cf-standard-names-linguistics
Most common n-grams
Overview
An n-gram is a sequence of length n of tokens (linguistic units). Here we take single words as the tokens to analyse.
Results
n-grams of set n without removal
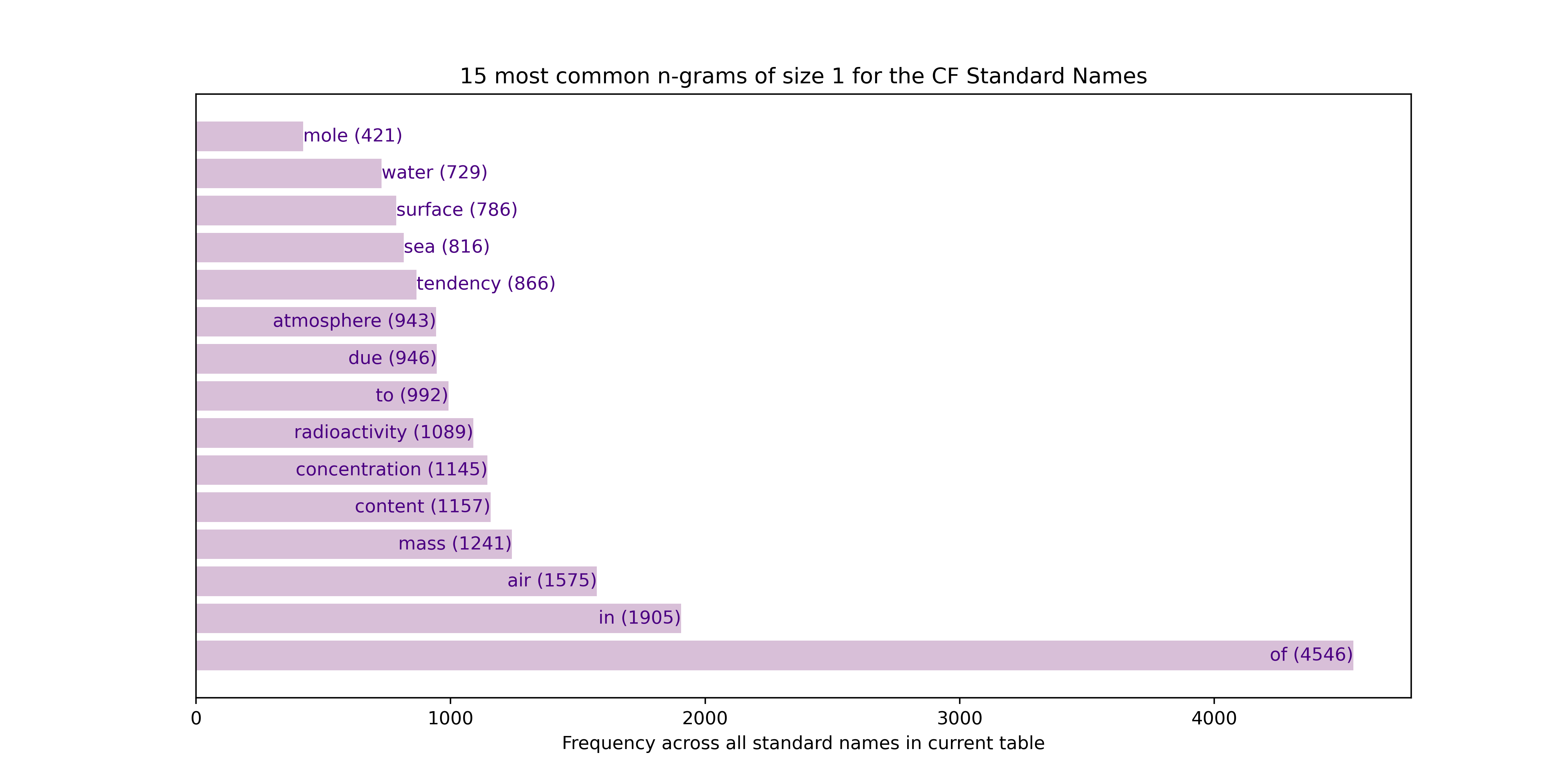
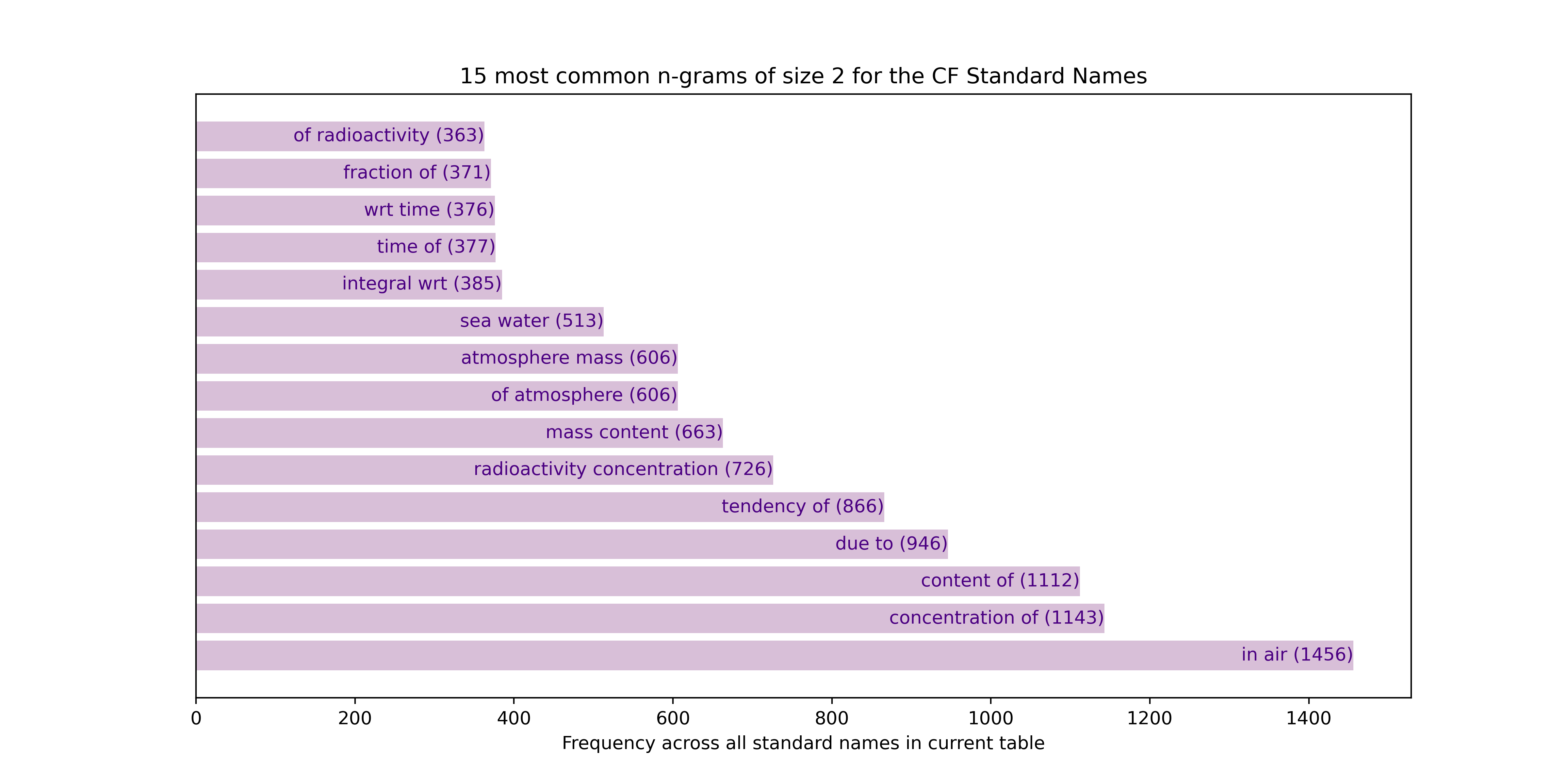
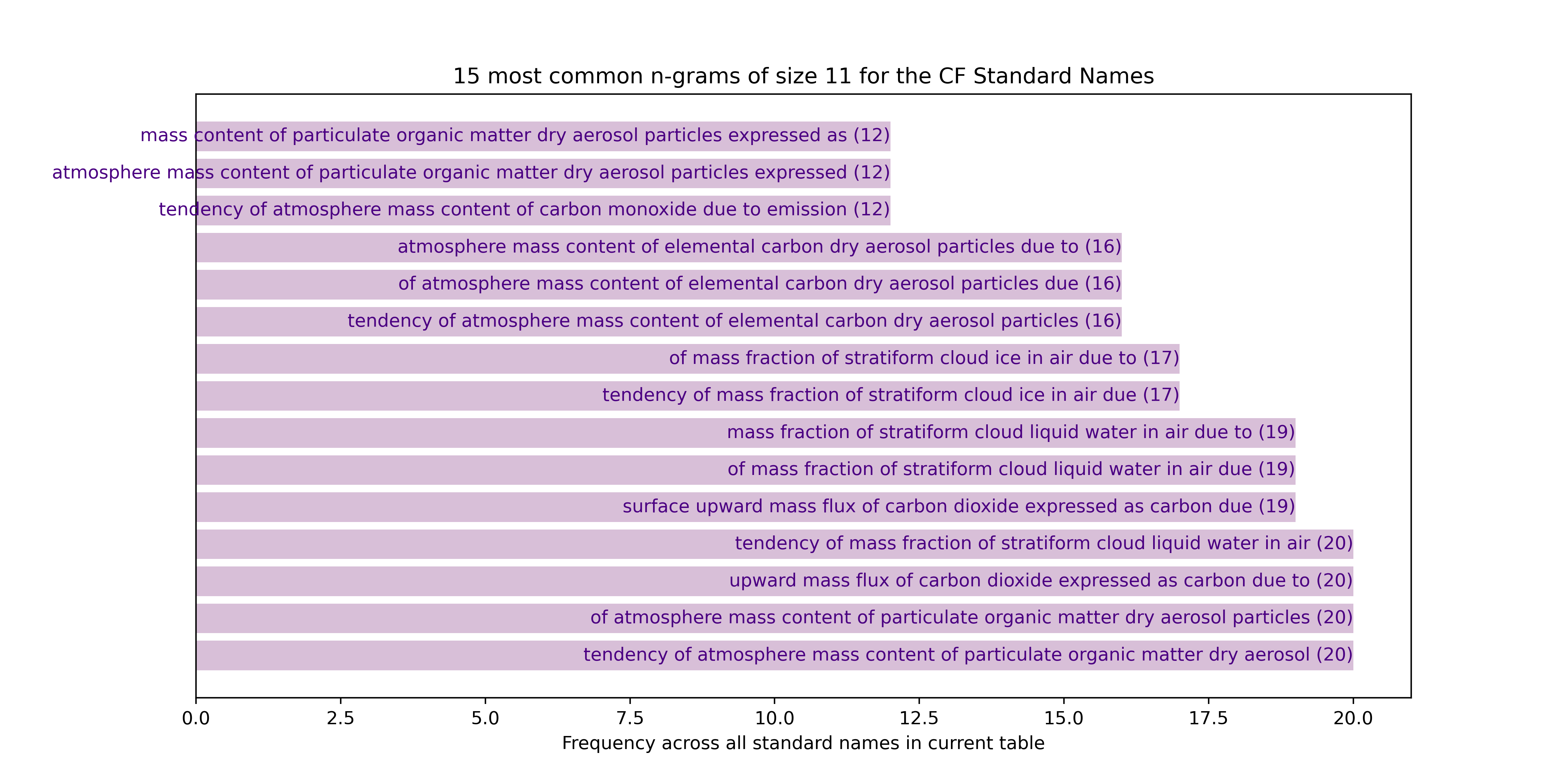
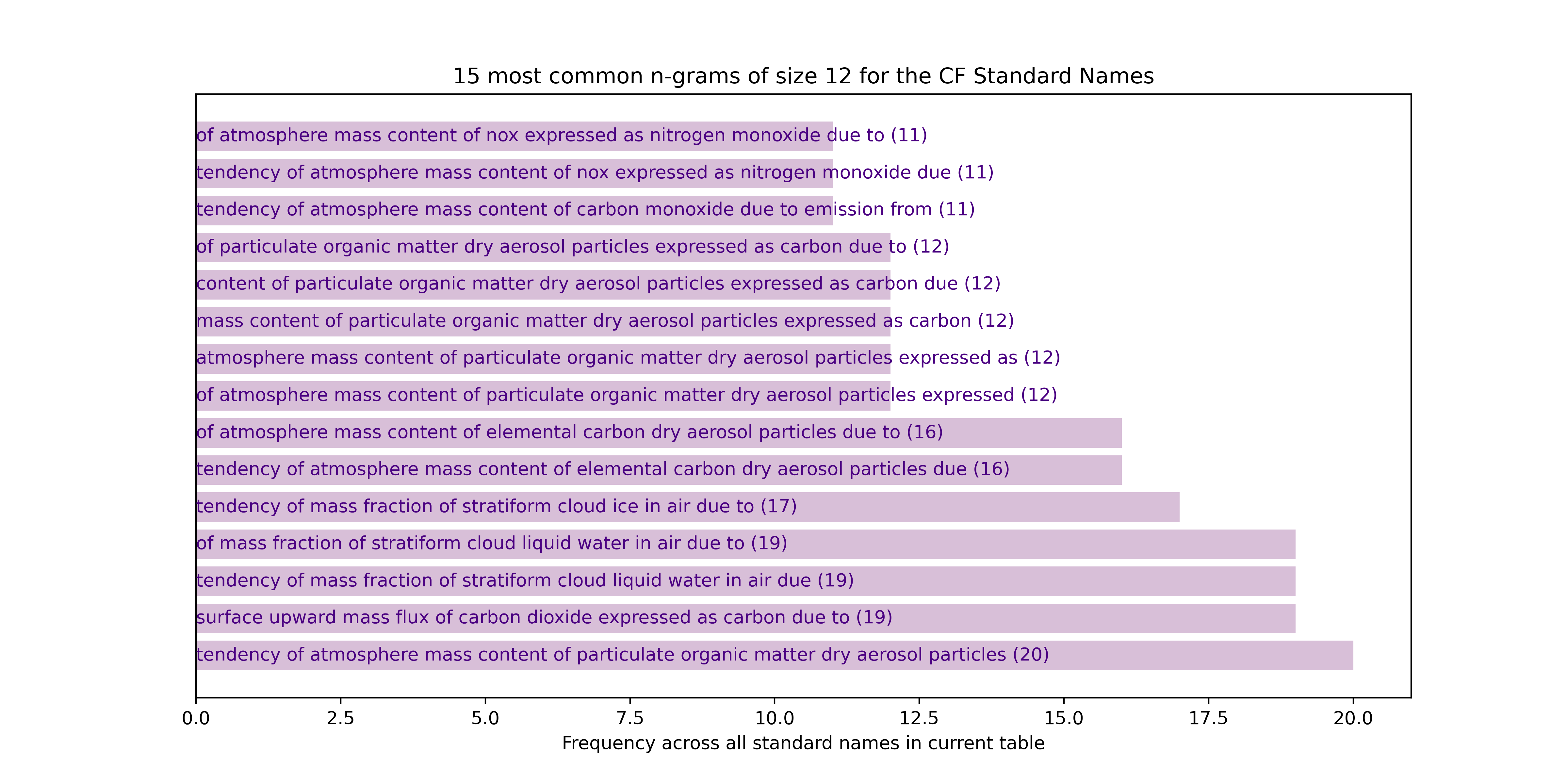
The most frequent n-grams of words in the full current (version 83 with data extracted on 30/11/23) Standard Names table of names for n = 1 to n = 20 words, are as follows (note the underscores in names have been replaced by whitespace to mimic natural text for enhanced readability):
Unigrams (1-grams i.e. single words)
Bigrams (2-grams)
Trigrams (3-grams)

4-grams

5-grams

6-grams

7-grams

8-grams

9-grams

10-grams

11-grams
12-grams
13-grams

14-grams

15-grams

16-grams

17-grams

18-grams

19-grams

20-grams

n-grams of higher n
After n=20 there are no more n-grams that occur more than once across all of the names, so further plots are not of interest. As an illustration, here is the plot of the next n, n=21:

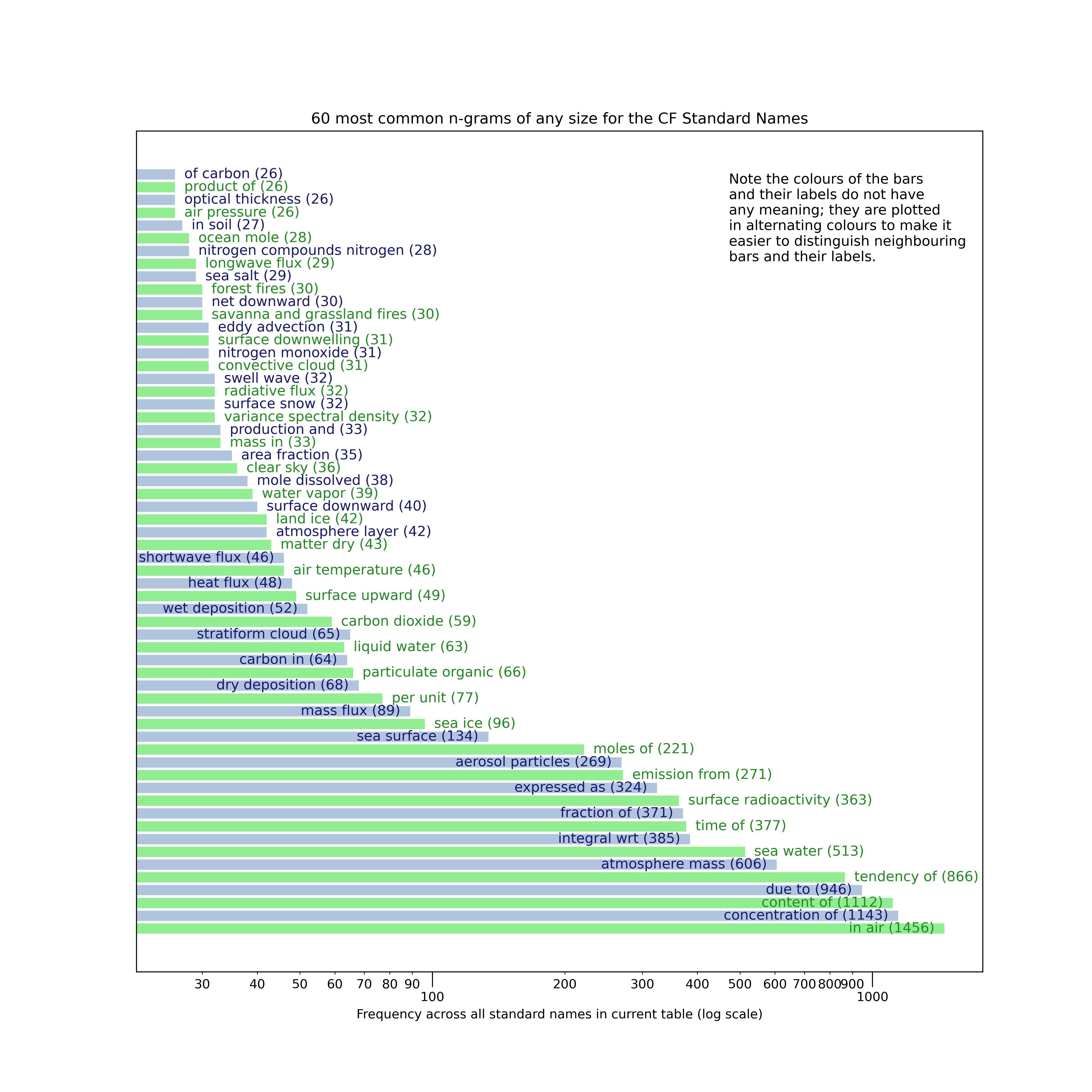
n-grams of any n with recursive removal
This time, consider n-grams of any length and follow a process of iterative removal, as follows:
- Find the n-grams of any length that occur most frequently within the full table of standard names (where underscores have been replaced with whitespace to mimic natural text for enhanced readability).
- If there is a single n-gram with the maximum frequency count in step (1),
use that as the input to step (3). Otherwise, in the case that multiple
n-grams are most common, take from this sub-list the n-gram(s) with
the highest n as inputs to step (3). Note the n-grams of lower
n discarded at this stage will be picked up in another iteration of
steps (1-) unless it is an n-gram contained in a larger n+N-gram
(for integer
N >= 1) e.g. ‘savanna and grassland’ contained in ‘savanna and grassland fires’ where the removal in step (3) will mean the n-gram is fully removed from the input names to the next iteration. (That way we keep and plot the longer n+N-gram for the results rather than the shorter one with the same count. This is preferred because the longer n+N-gram is more interesting, being a longer contiguous sequence. - Remove this most-common n-gram(2) determined in step (2) from all names and henceforth use the resultant reduced names as the names input;
- Go back to step (1), taking the names reduced under (2) as the new input names.
- Continue this process until the X most common n-grams of any length, excluding previous most-common n-grams which are incrementally removed, are found.
The results for the most common X=60, found by the above process, are as
follows: